Examples
Elastic Hex20
This example demonstrates how to convert a mesh from gmsh format to a meshio object and then translate that to a pyfebio mesh. The element and surface sets defined in the gmsh file are translated to lists of pyfebio Elements and Surfaces. Node sets are also created from the surfaces. A pyfebio Model is then instantiated with default values other than the mesh, which is specified as our translated mesh.
Each Elements object represents a part. We loop over these parts and assign a NeoHookean material and a SolidDomain to each. We assign a BCZeroDispacement boundary condition to the “bottom” node sets with all degrees of freedom active (fixing the bottom nodes in space).
We twist the top face by applying a BCRigidDeformation. The pos argument is a point on the axis of rotation, the rot argument is the rotation axis (its magnitude is the rotation angle, in this case \(\pi\) radians).
import meshio
import pyfebio as feb
# import a mesh from gmsh format
from_gmsh = meshio.gmsh.read("../../assets/gmsh/hex20.msh")
# use translation function to convert meshio object to an febio mesh
mesh = feb.mesh.translate_meshio(from_gmsh, node_sets_from_surfaces=True)
# creat a base febio model
my_model = feb.model.Model(mesh_=mesh)
# loop over the discovered Elements (parts) and assign materials
# and solid domains
for i, part in enumerate(my_model.mesh_.elements):
mat = feb.material.NeoHookean(
name=part.name,
E=feb.material.MaterialParameter(text=1.0 * (i + 1)),
v=feb.material.MaterialParameter(text=0.3),
)
my_model.material_.add_material(mat)
my_model.meshdomains_.add_solid_domain(feb.meshdomains.SolidDomain(name=part.name, mat=part.name))
# fix the bottom nodes in space
fix_bottom = my_model.boundary_.add_bc(feb.boundary.BCZeroDisplacement(node_set="bottom", x_dof=1, y_dof=1, z_dof=1))
# let's twist the top nodes by pi radians about their central z-axis
twist_top = my_model.boundary_.add_bc(
feb.boundary.BCRigidDeformation(node_set="top", pos="0.5,0.5,0.0", rot=feb.boundary.Value(lc=1, text="0.0,0.0,3.14"))
)
# the load curve for our twist
my_model.loaddata_.add_load_curve(feb.loaddata.LoadCurve(id=1, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "1.0,1.0"])))
# save the model
my_model.save("elastic_hex20.feb")
# run the model
feb.model.run_model("elastic_hex20.feb")
The maximum Green-Lagrange shear strain after twisting the top face by \(\pi\) radians. Note the top layer is 2X stiffer than the bottom layer.
Biphasic Hex20
Most steps are similar to the Elastic Hex20 example. We instead instantiate a pyfebio BiphasicModel, which sets the module to “biphasic”, the analysis to “TRANSIENT”, and the solver type to “biphasic”. We assign a BiphasicMaterial with a NeoHookean solid phase and ConstantIsoPerm as the permeability. The bottom nodes are fixed in space, a BCZeroFluidPressure boundary condition to allow free-draining on the top surface, and a BCPrescribedDisplacement in the z direction for the top nodes.
from meshio.gmsh import read
import pyfebio as feb
# import mesh from gmsh format
from_gmsh = read("../../assets/gmsh/hex20.msh")
# translate meshio mesh to febio mesh
mesh = feb.mesh.translate_meshio(from_gmsh, node_sets_from_surfaces=True)
# initialize a biphasic febio modelk
my_model = feb.model.BiphasicModel(mesh_=mesh)
assert my_model.control_ is not None
my_model.control_.step_size = 0.1
my_model.control_.time_stepper = feb.control.TimeStepper(dtmax=feb.control.TimeStepValue(text=1.0))
# loop over Elements (parts) and assign biphasic materials
# and also assign solid domains
for i, part in enumerate(my_model.mesh_.elements):
mat = feb.material.BiphasicMaterial(
name=part.name,
solid=feb.material.NeoHookean(),
permeability=feb.material.ConstantIsoPerm(perm=feb.material.MaterialParameter(text=1e-3 * (i + 1))),
)
my_model.material_.add_material(mat)
my_model.meshdomains_.add_solid_domain(feb.meshdomains.SolidDomain(name=part.name, mat=part.name))
# fix the bottom nodes in space
fix_bottom = my_model.boundary_.add_bc(feb.boundary.BCZeroDisplacement(node_set="bottom", x_dof=1, y_dof=1, z_dof=1))
# set zero fluid pressure bc on bottom nodes to allow for free-draining
drain_bottom = my_model.boundary_.add_bc(feb.boundary.BCZeroFluidPressure(node_set="bottom"))
# set zero fluid pressure bc on top nodes to allow for free-draining
drain_top = my_model.boundary_.add_bc(feb.boundary.BCZeroFluidPressure(node_set="top"))
# displace the top nodes by -0.5 mm in z
move_top = my_model.boundary_.add_bc(
feb.boundary.BCPrescribedDisplacement(node_set="top", dof="z", value=feb.boundary.Value(lc=1, text=-0.5))
)
# load curve to apply displacement
my_model.loaddata_.add_load_curve(feb.loaddata.LoadCurve(id=1, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "0.1,1.0", "10.0,1.0"])))
# add some additonial variables to plotfile
my_model.output_.add_plotfile(
feb.output.OutputPlotfile(
all_vars=[
feb.output.Var(type="displacement"),
feb.output.Var(type="effective fluid pressure"),
feb.output.Var(type="nodal fluid flux"),
feb.output.Var(type="Lagrange strain"),
]
)
)
# save the model to disk
my_model.save("biphasic_hex20.feb")
# run the model
feb.model.run_model("biphasic_hex20.feb")
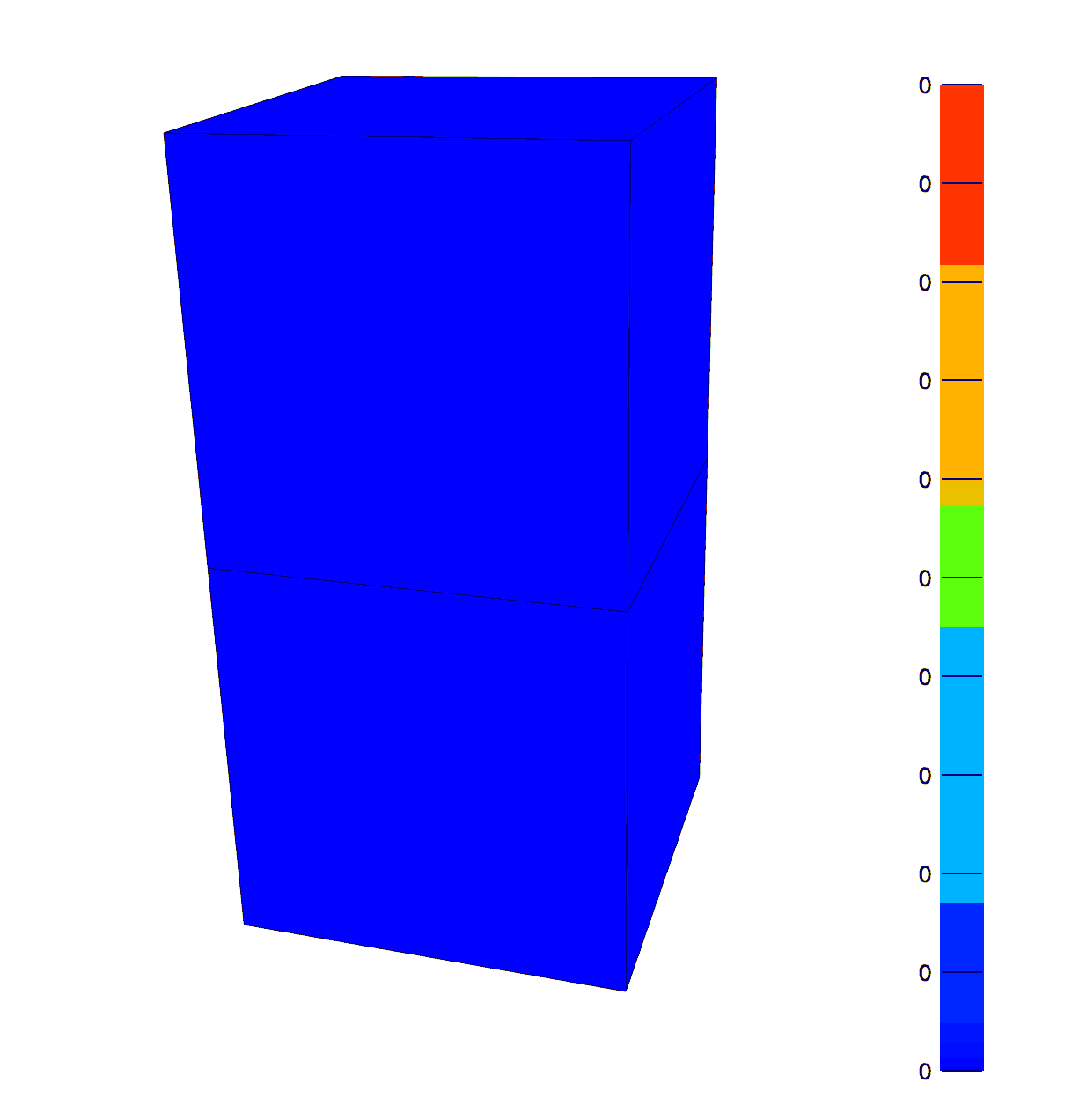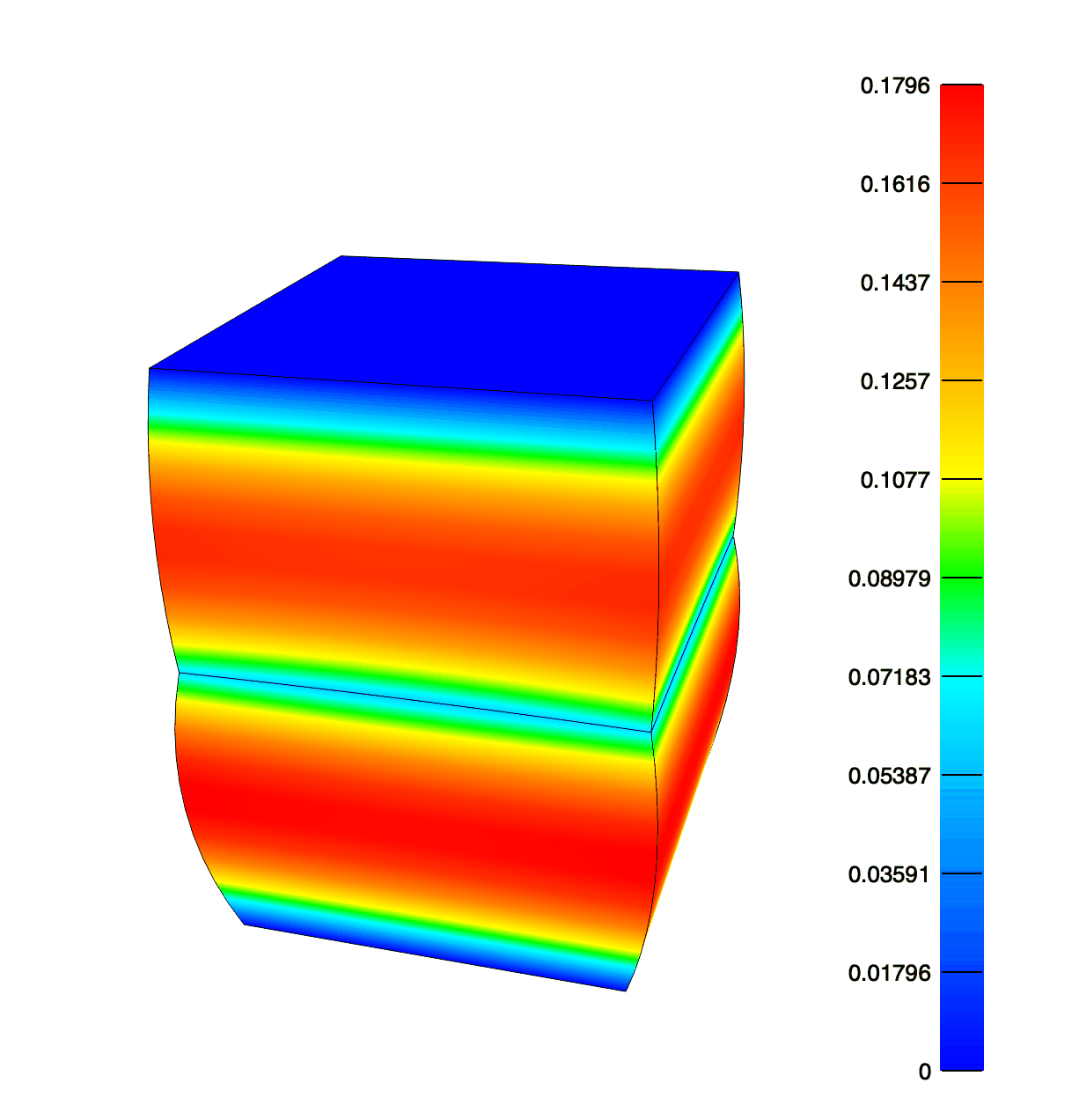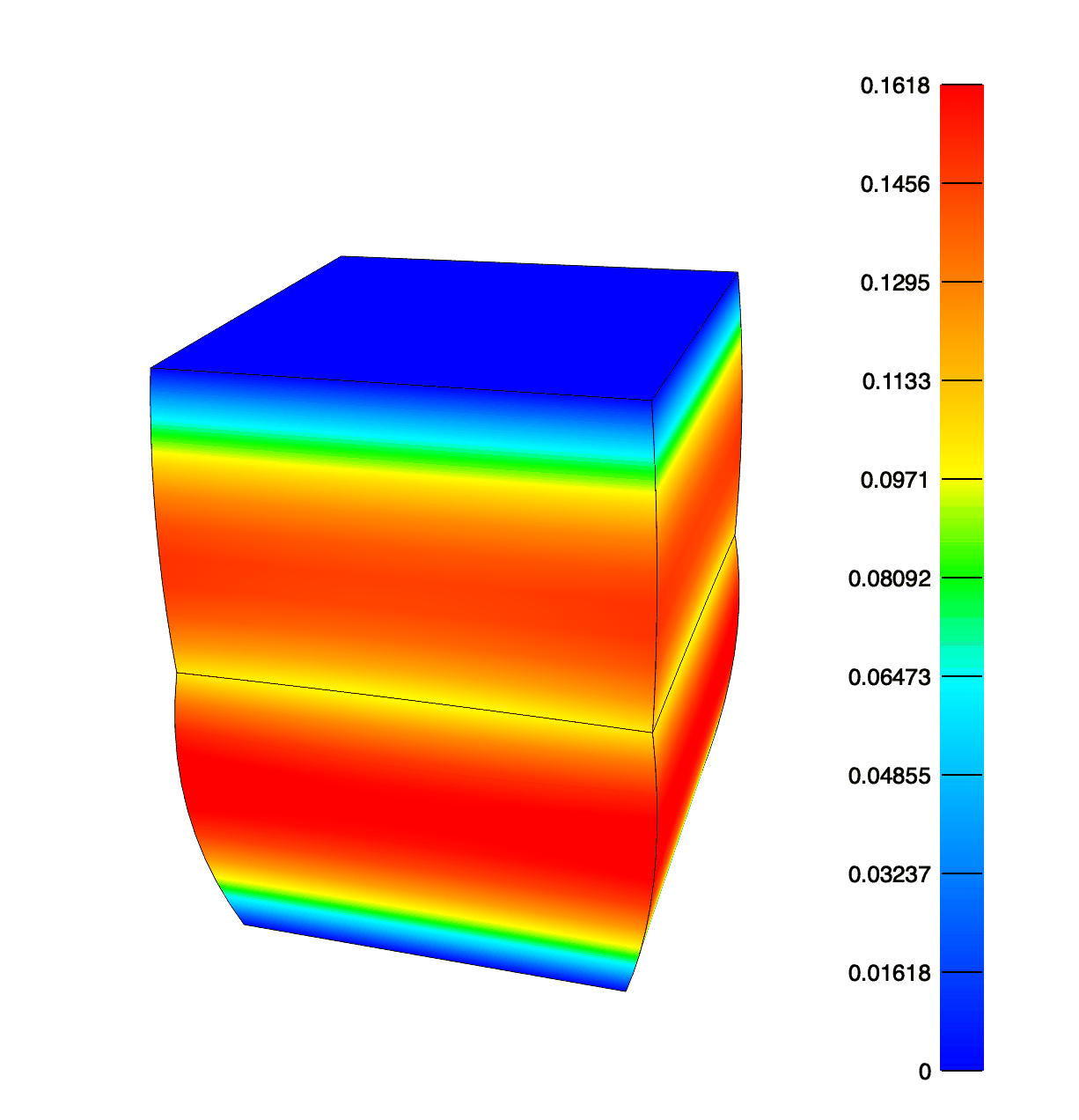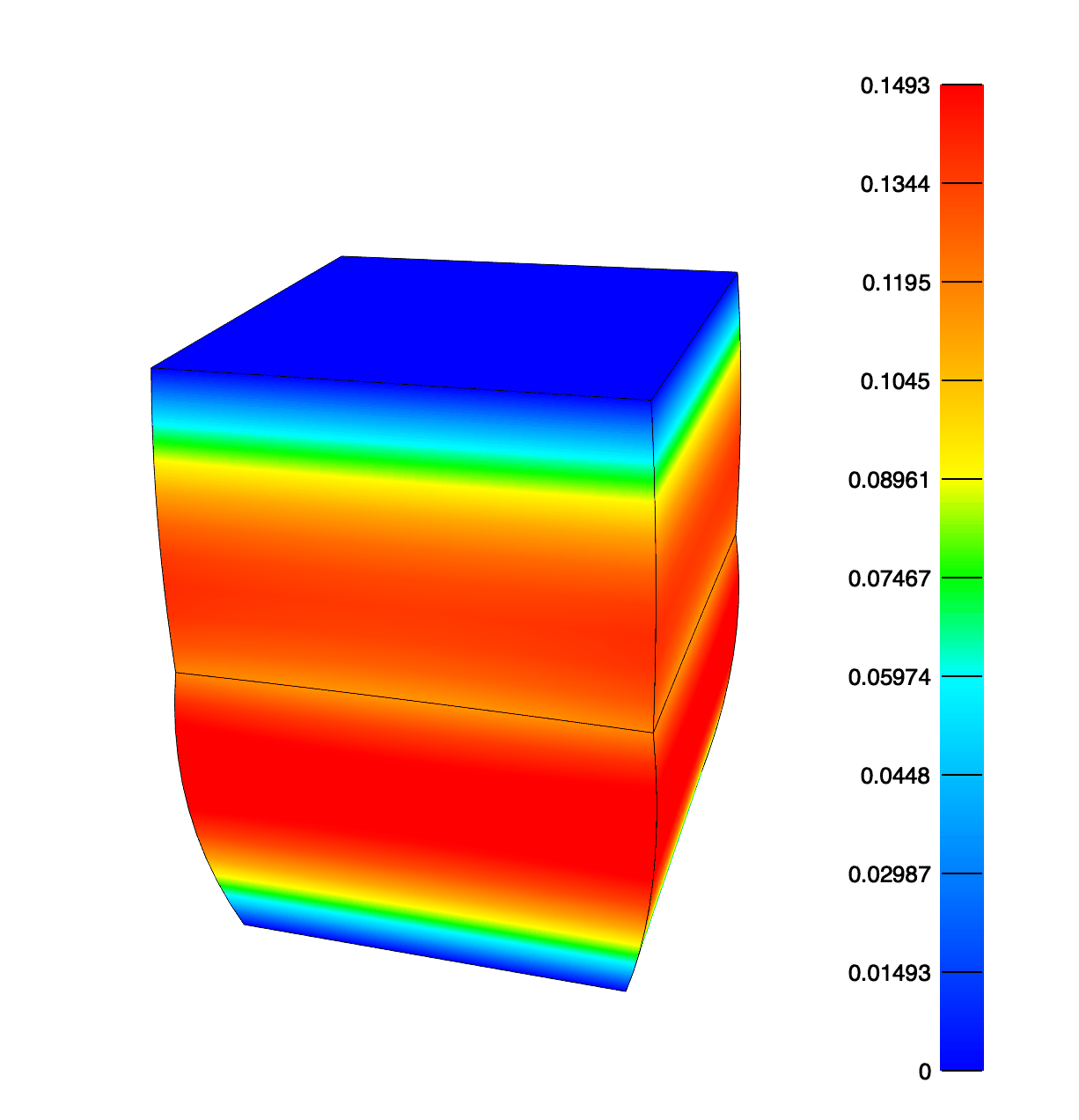
The effective fluid pressure after compressing the top face by 0.5mm in 0.1 seconds and then holding for 9.9 seconds. Note that the top element has twice the permeability of the bottom, hence the asymmetry in fluid pressure and deformation.
Sliding Contact
This example demonstrates sliding contact. This requires the definition of a SurfacePair, which is then referenced in the SlidingElastic contact definition. We enforce the contact constraint with the augmented Lagrange multiplier method by setting laugon=”AUGLAG”. We also set two_pass=1, which helps reduce penetration at the sharp edges of this very coarse mesh.
import meshio
import pyfebio as feb
# read a 27 node hex mesh in gmsh format
from_gmsh = meshio.gmsh.read("../../assets/gmsh/hex27_contact.msh")
# translate gmsh meshio object to an febio mesh
mesh = feb.mesh.translate_meshio(from_gmsh, node_sets_from_surfaces=True)
# initialize and febio model with default settings
my_model = feb.model.Model(mesh_=mesh)
# loop over the mesh Elements (parts) and assign materials
# and solid domains
for part in my_model.mesh_.elements:
mat = feb.material.NeoHookean(
name=part.name,
E=feb.material.MaterialParameter(text=1.0),
v=feb.material.MaterialParameter(text=0.3),
)
my_model.material_.add_material(mat)
my_model.meshdomains_.add_solid_domain(feb.meshdomains.SolidDomain(name=part.name, mat=part.name))
# add a surface pair for the contact definition
my_model.mesh_.add_surface_pair(feb.mesh.SurfacePair(name="contact", primary="bottom-box-top", secondary="top-box-bottom"))
# fix the bottom nodes of the bottom box in space
my_model.boundary_.add_bc(feb.boundary.BCZeroDisplacement(node_set="bottom-box-bottom", x_dof=1, y_dof=1, z_dof=1))
# fix the top nodes of the top box in the y dimension
my_model.boundary_.add_bc(feb.boundary.BCZeroDisplacement(node_set="top-box-top", x_dof=0, y_dof=1, z_dof=0))
# move the top nodes of the top box in the the dimension
my_model.boundary_.add_bc(
feb.boundary.BCPrescribedDisplacement(node_set="top-box-top", dof="z", value=feb.boundary.Value(lc=1, text=-0.15))
)
# move the top nodes of the top box in the x dimension
my_model.boundary_.add_bc(feb.boundary.BCPrescribedDisplacement(node_set="top-box-top", dof="x", value=feb.boundary.Value(lc=1, text=0.3)))
# add a sliding contact definition. enforce it with augmented lagrangian multiplier
my_model.contact_.add_contact(
feb.contact.SlidingElastic(name="sliding_contact", surface_pair="contact", auto_penalty=1, laugon="AUGLAG", two_pass=1)
)
# load curve controlling the top nodes displacement
my_model.loaddata_.add_load_curve(feb.loaddata.LoadCurve(id=1, points=feb.loaddata.CurvePoints(points=["0,0", "1,1"])))
# add variables to the plotfile output
my_model.output_.add_plotfile(
feb.output.OutputPlotfile(
all_vars=[
feb.output.Var(type="displacement"),
feb.output.Var(type="contact pressure"),
feb.output.Var(type="contact gap"),
feb.output.Var(type="Lagrange strain"),
]
)
)
# save the model to disk
my_model.save("contact.feb")
# run the model
feb.model.run_model("contact.feb")
The z-displacement resulting from the contact simulation. Note the nodal penetration near the sharp edge due to the coarse mesh size. This is more severe if the penalty method is used or two_pass is turned off.
Adaptive Remeshing
FEBio has several implementations of adaptive remeshing. This example demonstrates an adaptor that will refine a hex8 mesh to reduce the stress error in the bottom-layer.
import meshio
import pyfebio as feb
# import an 8 node hex mesh in gmsh format
from_gmsh = meshio.gmsh.read("../../assets/gmsh/hex8.msh")
# convert the meshio object to febio mesh
mesh = feb.mesh.translate_meshio(from_gmsh, node_sets_from_surfaces=True)
# crete a base febio model but override the control section to have constant time step
my_model = feb.model.Model(mesh_=mesh, control_=feb.control.Control(time_steps=10, step_size=0.1, time_stepper=None))
# loop over all Elements in the mesh and assign materials and solid domains
for i, part in enumerate(my_model.mesh_.elements):
mat = feb.material.NeoHookean(
name=part.name,
E=feb.material.MaterialParameter(text=10.0 * (i + 1)),
v=feb.material.MaterialParameter(text=0.3),
)
my_model.material_.add_material(mat)
my_model.meshdomains_.add_solid_domain(feb.meshdomains.SolidDomain(name=part.name, mat=part.name))
# fix the bottom nodes
fix_bottom = my_model.boundary_.add_bc(feb.boundary.BCZeroDisplacement(node_set="bottom", x_dof=1, y_dof=1, z_dof=1))
# displace the top nodes in z by -0.5 mm
move_top = my_model.boundary_.add_bc(
feb.boundary.BCPrescribedDisplacement(node_set="top", dof="z", value=feb.boundary.Value(lc=1, text=0.5))
)
# load curve controlling the top nodes displacement
my_model.loaddata_.add_load_curve(feb.loaddata.LoadCurve(id=1, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "1.0,1.0"])))
# creat are mesh adaptor to refine the mesh based
# on the stress error criterion
adaptor = feb.meshadaptor.HexRefineAdaptor(
elem_set="bottom-layer",
max_iters=1,
max_elements=10000,
criterion=feb.meshadaptor.RelativeErrorCriterion(error=0.01, data=feb.meshadaptor.StressCriterion()),
)
my_model.meshadaptor_.add_adaptor(adaptor)
# we have to add the stress error output to the plotfile so our mesh
# adaptor works
my_model.output_.add_plotfile(
feb.output.OutputPlotfile(
all_vars=[
feb.output.Var(type="displacement"),
feb.output.Var(type="stress error"),
]
)
)
# save our madel to disk
my_model.save("mesh_adapt.feb")
# run the model
feb.model.run_model("mesh_adapt.feb")
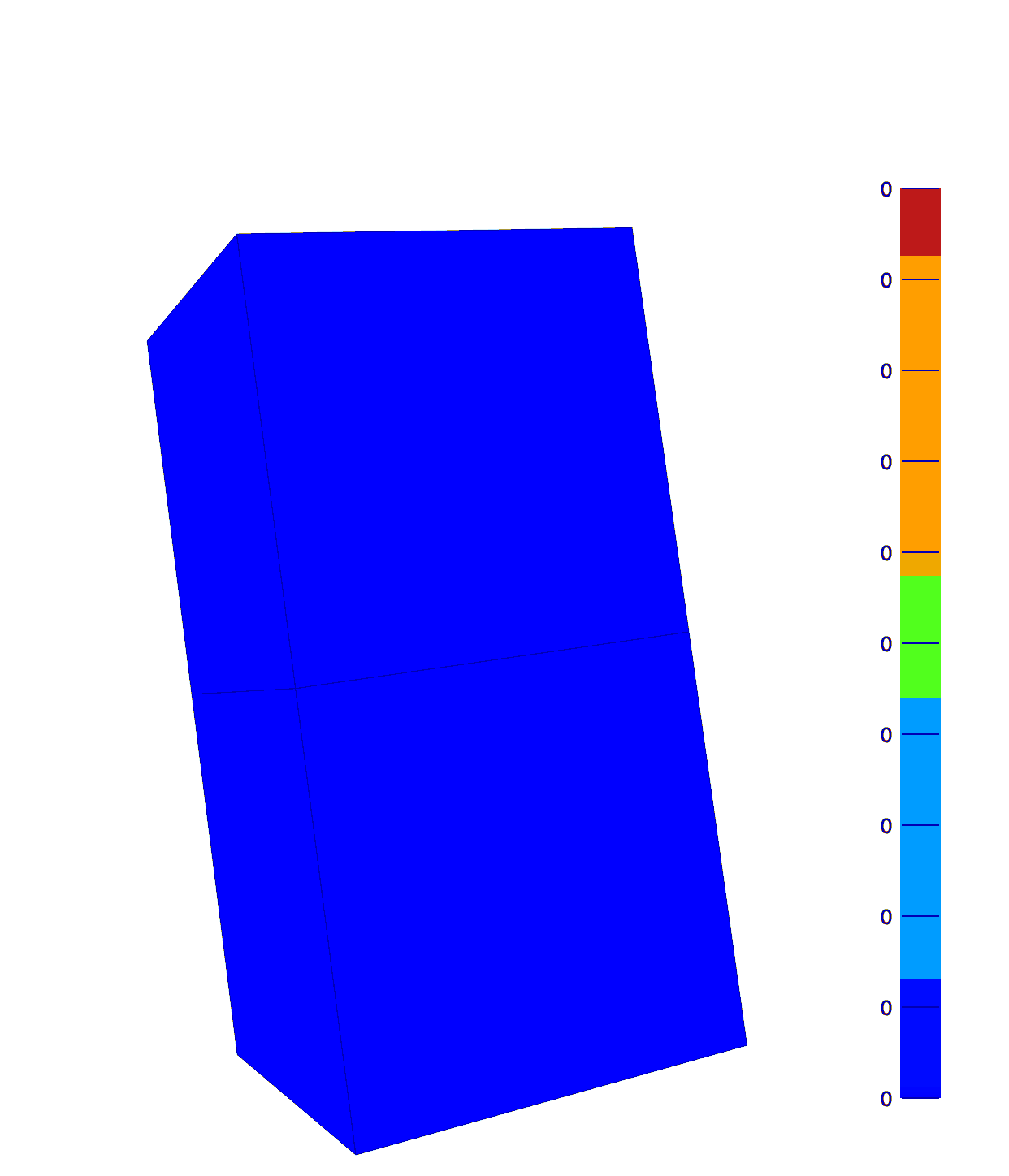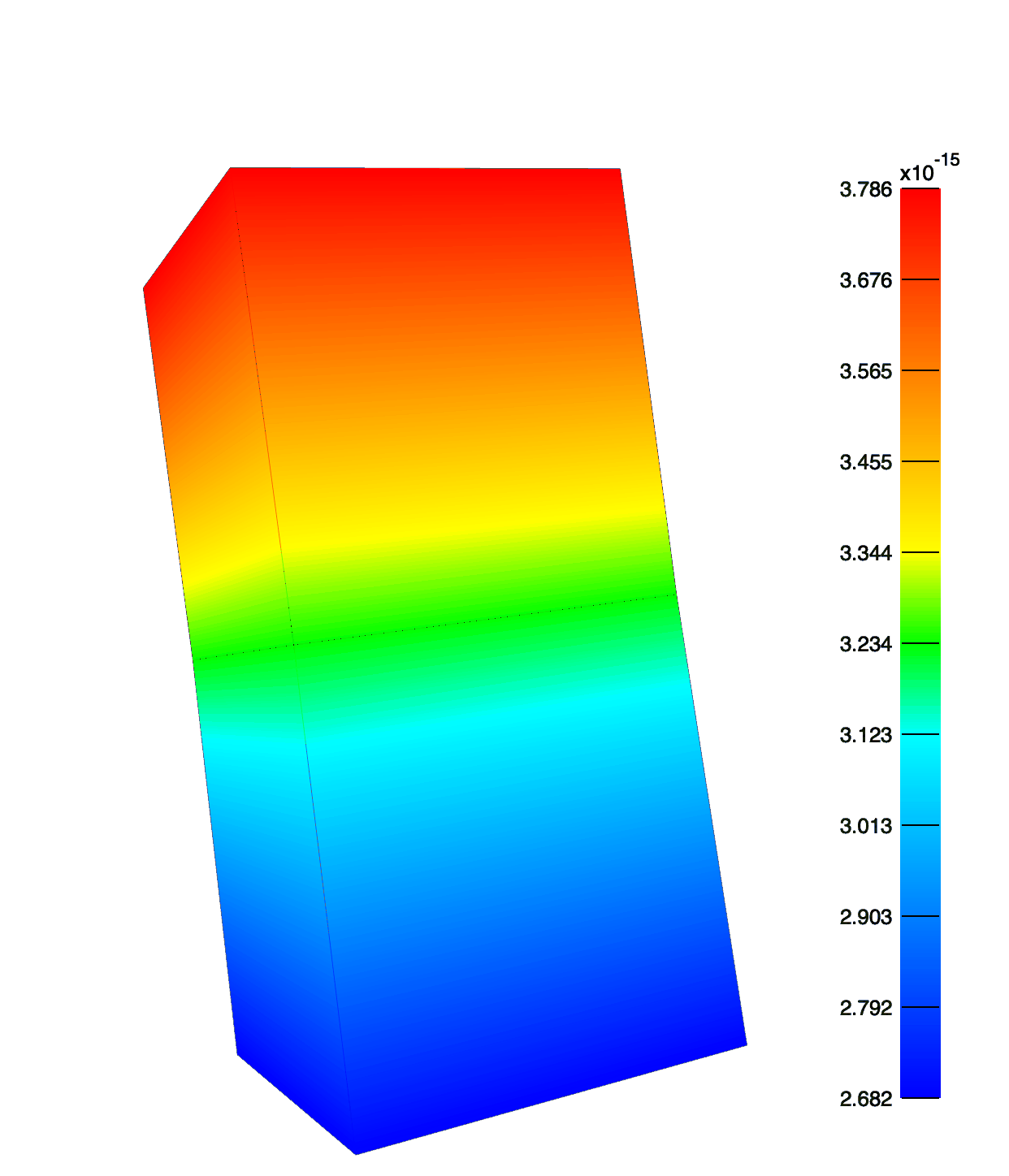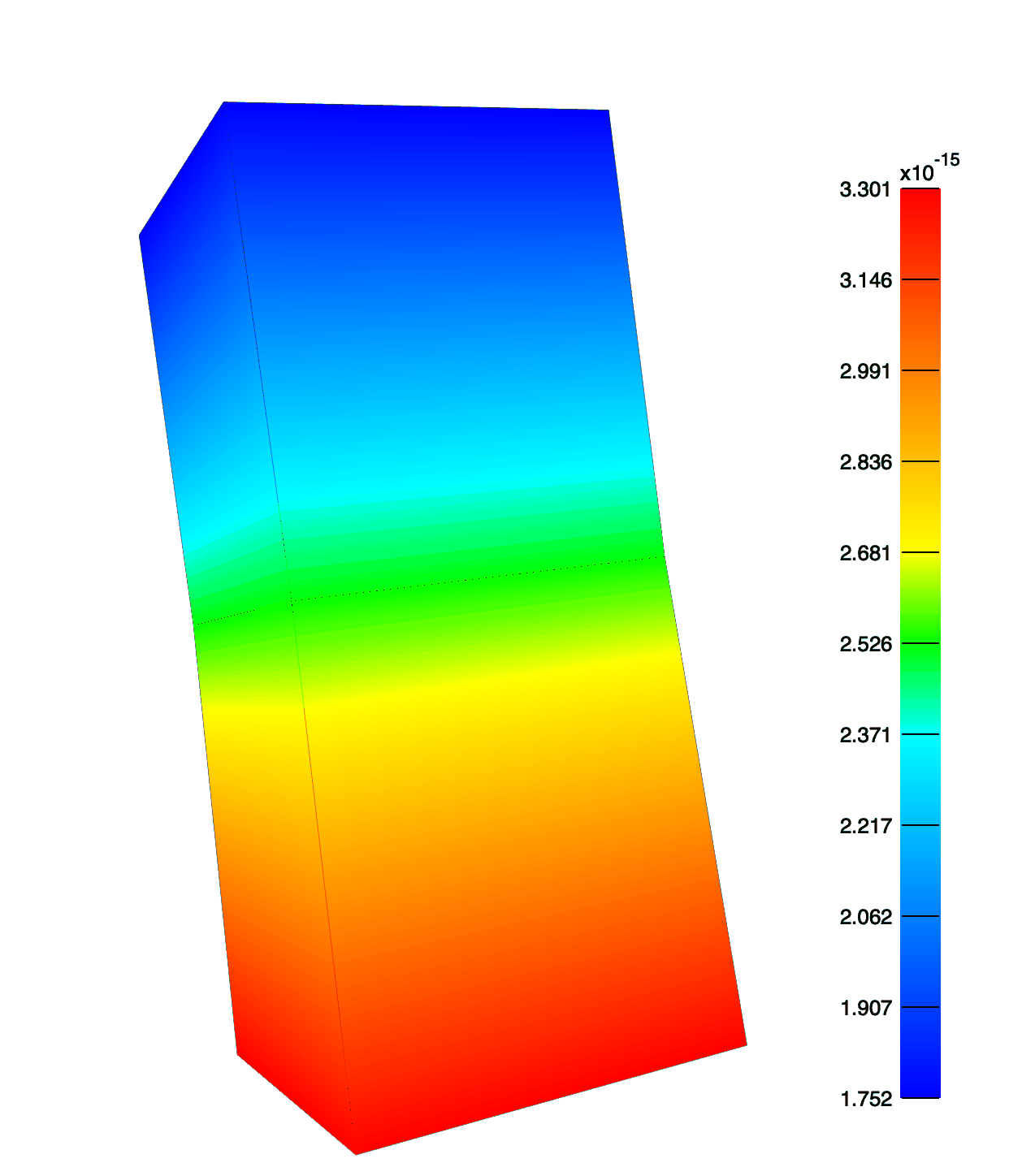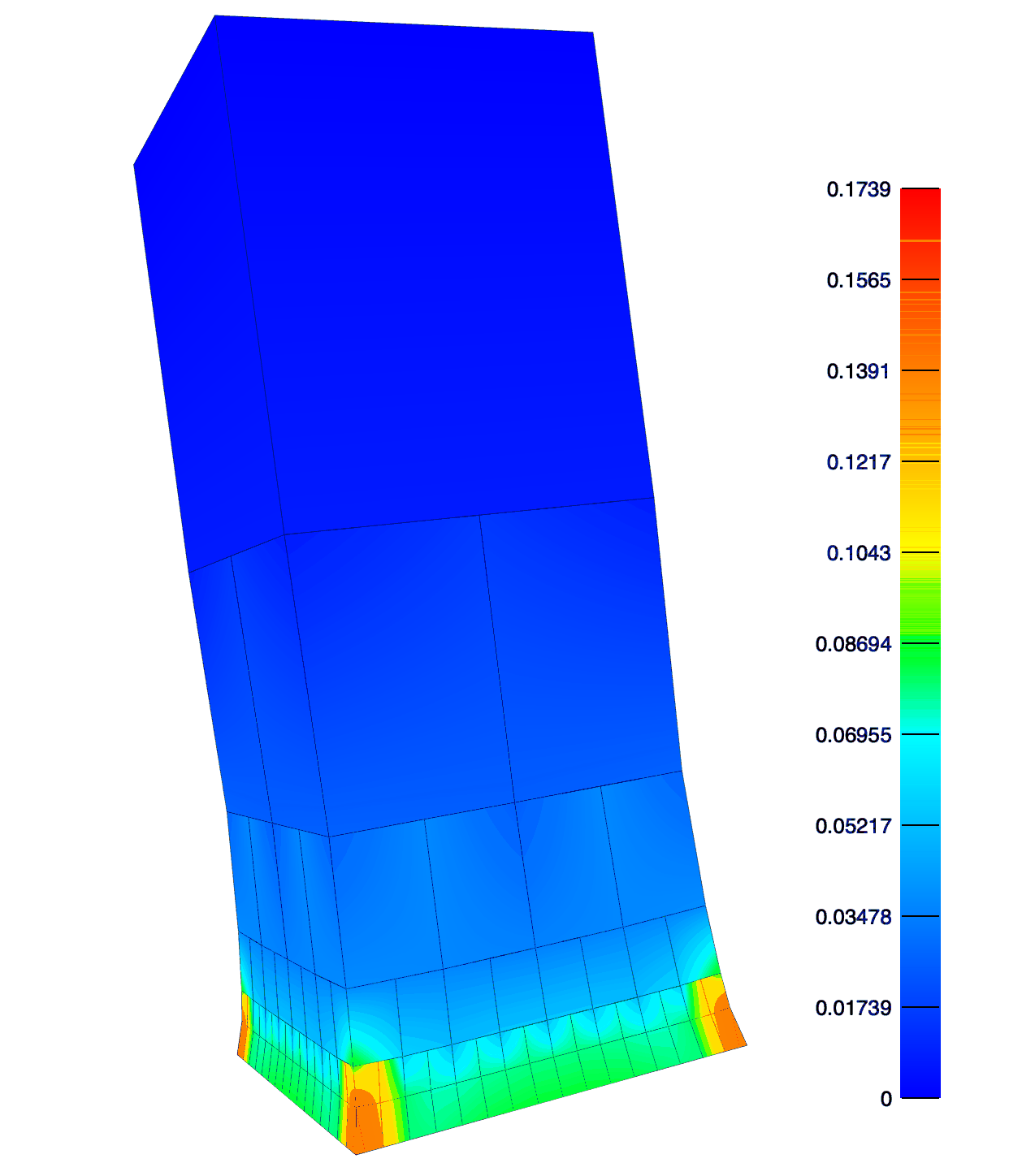
The hex mesh adaptively refines to reduce the stress error in the bottom-layer. Note the greatest refinement occurs at the necking corners.
Three Cylinder Joint
This example demonstrates the use of rigid connectors to create a three cylinder linkage, which is a popular approach to modeling joint dynamics.
import pyfebio as feb
# manually create the nodes
all_nodes = [
feb.mesh.Node(id=1, text="-2.0,-1.0,-10"),
feb.mesh.Node(id=2, text="2.0,-1.0,-10"),
feb.mesh.Node(id=3, text="2.0,1.0,-10"),
feb.mesh.Node(id=4, text="-2.0,1.0,-10"),
feb.mesh.Node(id=5, text="-2.0,-1.0,0"),
feb.mesh.Node(id=6, text="2.0,-1.0,0"),
feb.mesh.Node(id=7, text="2.0,1.0,0"),
feb.mesh.Node(id=8, text="-2.0,1.0,0"),
feb.mesh.Node(id=9, text="-2.0,-1.0,0"),
feb.mesh.Node(id=10, text="2.0,-1.0,0"),
feb.mesh.Node(id=11, text="2.0,1.0,0"),
feb.mesh.Node(id=12, text="-2.0,1.0,0"),
feb.mesh.Node(id=13, text="-2.0,-1.0,10"),
feb.mesh.Node(id=14, text="2.0,-1.0,10"),
feb.mesh.Node(id=15, text="2.0,1.0,10"),
feb.mesh.Node(id=16, text="-2.0,1.0,10"),
]
# create a Nodes object
nodes = feb.mesh.Nodes(name="Nodes", all_nodes=all_nodes)
# create Hex8Element for rigid bodies
# each of these is a separate Elements object
# so they are unique parts
body_a = feb.mesh.Elements(name="BodyA", type="hex8", all_elements=[feb.mesh.Hex8Element(id=1, text="1,2,3,4,5,6,7,8")])
body_b = feb.mesh.Elements(name="BodyB", type="hex8", all_elements=[feb.mesh.Hex8Element(id=2, text="9,10,11,12,13,14,15,16")])
# create the base model
my_model = feb.model.Model()
# add the Nodes
my_model.mesh_.add_node_domain(nodes)
# add the Elements (parts)
my_model.mesh_.add_element_domain(body_a)
my_model.mesh_.add_element_domain(body_b)
# create rigid body materials for BodyA and BodyB
my_model.material_.add_material(feb.material.RigidBody(name="BodyA", center_of_mass="0,0,0"))
my_model.material_.add_material(feb.material.RigidBody(name="BodyB", center_of_mass="0,0,0"))
# assign solid domains to the rigid bodies
my_model.meshdomains_.add_solid_domain(feb.meshdomains.SolidDomain(name="BodyA", mat="BodyA"))
my_model.meshdomains_.add_solid_domain(feb.meshdomains.SolidDomain(name="BodyB", mat="BodyB"))
# we need two more rigid bodies for the purpose of creating our
# three cylinder linkage. We use the convenience function
# add_simple_rigid_body() to create these
my_model.add_simple_rigid_body(origin=(0.0, 0.0, 0.0), name="GhostA")
my_model.add_simple_rigid_body(origin=(0.0, 0.0, 0.0), name="GhostB")
# fix BodyA in space
my_model.rigid_.add_rigid_bc(feb.rigid.RigidFixed(rb="BodyA", Rx_dof=1, Ry_dof=1, Rz_dof=1, Ru_dof=1, Rw_dof=1, Rv_dof=1))
# define a RigidCylindricalJoint connector between BodyA and GhostA
# this is the internal-external rotation / inferior-superior translation axis
# prescribe rotation and translation
my_model.rigid_.add_rigid_connector(
feb.rigid.RigidCylindricalJoint(
name="IERot_ISTranslation",
body_a="BodyA",
body_b="GhostA",
joint_axis="0.0,0.0,1.0",
transverse_axis="1.0,0.0,0.0",
prescribed_rotation=1,
prescribed_translation=1,
rotation=feb.rigid.Value(lc=1, text=1.57),
translation=feb.rigid.Value(lc=2, text=1.0),
)
)
# define a RigidCylindricalJoint connector between GhostA and GhostB
# this is the varus-valgus rotation / anterior-posterior translation axis
# prescribe rotation and translation
my_model.rigid_.add_rigid_connector(
feb.rigid.RigidCylindricalJoint(
name="VVRot_APTranslation",
body_a="GhostA",
body_b="GhostB",
joint_axis="0.0,1.0,0.0",
transverse_axis="1.0,0.0,0.0",
prescribed_rotation=1,
prescribed_translation=1,
rotation=feb.rigid.Value(lc=3, text=1.57),
translation=feb.rigid.Value(lc=4, text=1.0),
)
)
# define a RigidCylindricalJoint connector between GhostB and BodyB
# this is the flexion-extension rotation / medial-lateral translation axis
# prescribe rotation and translation
my_model.rigid_.add_rigid_connector(
feb.rigid.RigidCylindricalJoint(
name="Flexion_MLTranslation",
body_a="GhostB",
body_b="BodyB",
joint_axis="1.0,0.0,0.0",
transverse_axis="0.0,0.0,1.0",
prescribed_rotation=1,
prescribed_translation=1,
rotation=feb.rigid.Value(lc=5, text=1.57),
translation=feb.rigid.Value(lc=6, text=1.0),
)
)
# load curve for internal-external rotation
my_model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=1, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "0.5,1.0", "1.5,-1.0", "2.0,0.0"]))
)
# load curve for inferior-superior translation
my_model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=2, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "2.0,0.0", "2.5,1.0", "3.5,-1.0", "4.0,0.0"]))
)
# load curve for varus-valgus rotation
my_model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=3, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "4.0,0.0", "4.5,1.0", "5.5,-1.0", "6.0,0.0"]))
)
# load curve for anterior-posterior translation
my_model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=4, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "6.0,0.0", "6.5,1.0", "7.5,-1.0", "8.0,0.0"]))
)
# load curve for flexion-extension rotation
my_model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=5, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "8.0,0.0", "8.5,1.0", "9.5,-1.0", "10.0,0.0"]))
)
# load curve for medial-lateral translation
my_model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=6, points=feb.loaddata.CurvePoints(points=["0.0,0.0", "10.0,0.0", "10.5,1.0", "11.5,-1.0", "12.0,0.0"]))
)
# must point load curve; note interpolate="STEP"
my_model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(
id=7,
interpolate="STEP",
points=feb.loaddata.CurvePoints(points=[f"{i * 0.25},0.25" for i in range(48)]),
)
)
# change the number of time steps and step_size
# to cover 12 second simulation time
my_model.control_ = feb.control.Control(time_steps=24, step_size=0.5)
# set dtmax of time_stepper to must point load curve
# this guarantees we have a solution at the beginning and end of
# each dof trajectory
my_model.control_.time_stepper.dtmax = feb.control.TimeStepValue(lc=7, text=0.5)
# save and run the model
my_model.save("three_cylinder_joint.feb")
feb.model.run_model("three_cylinder_joint.feb")
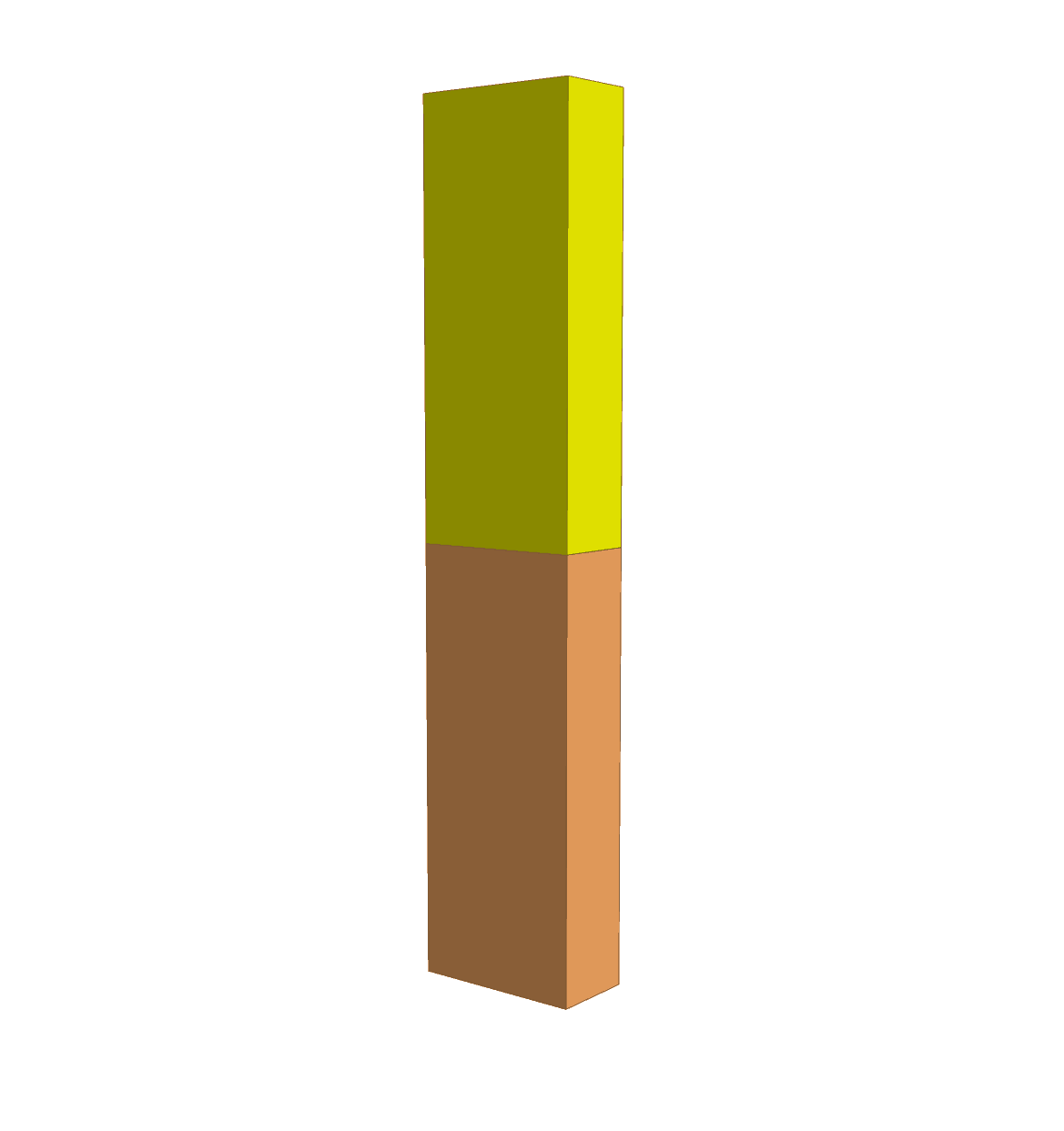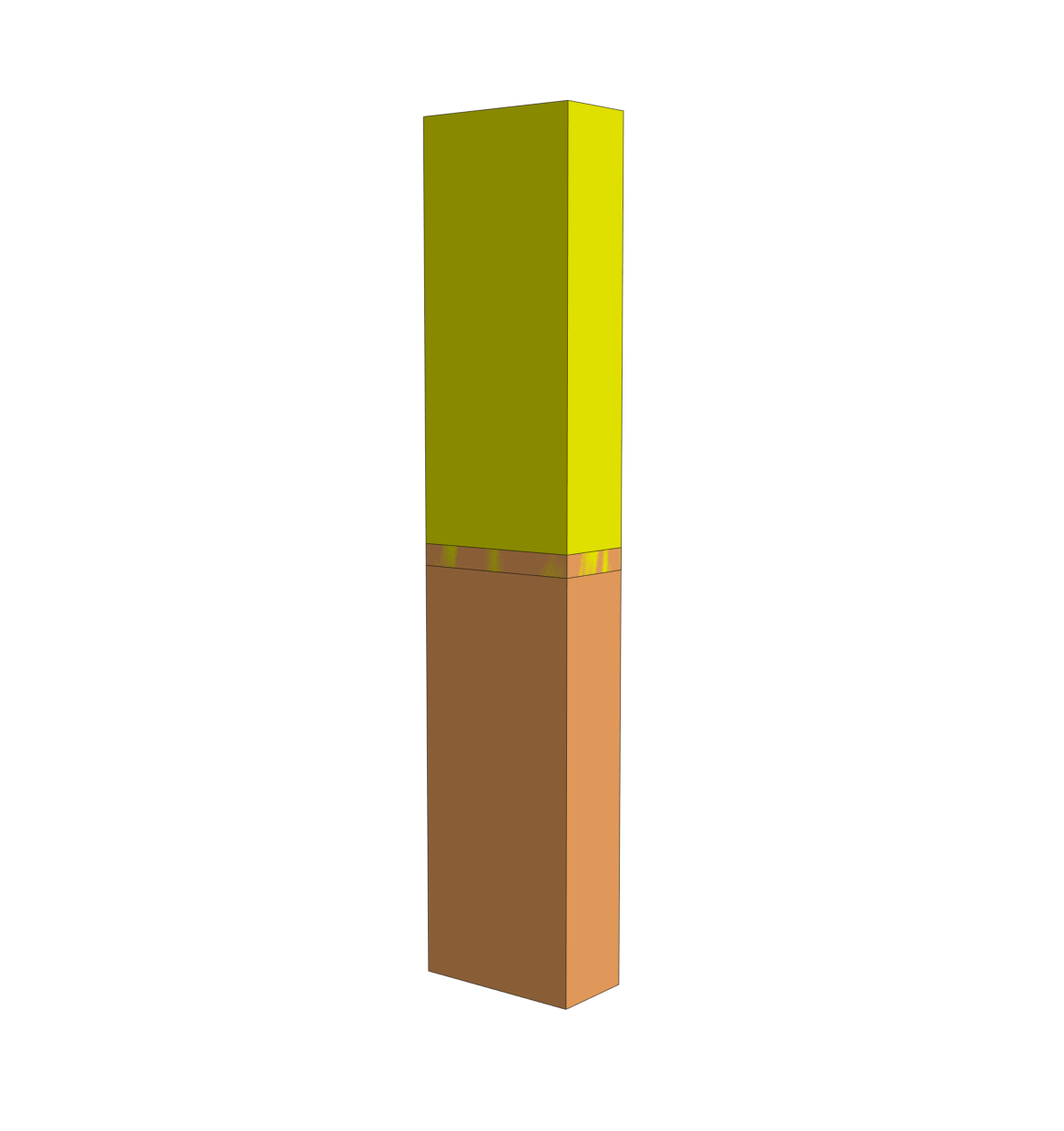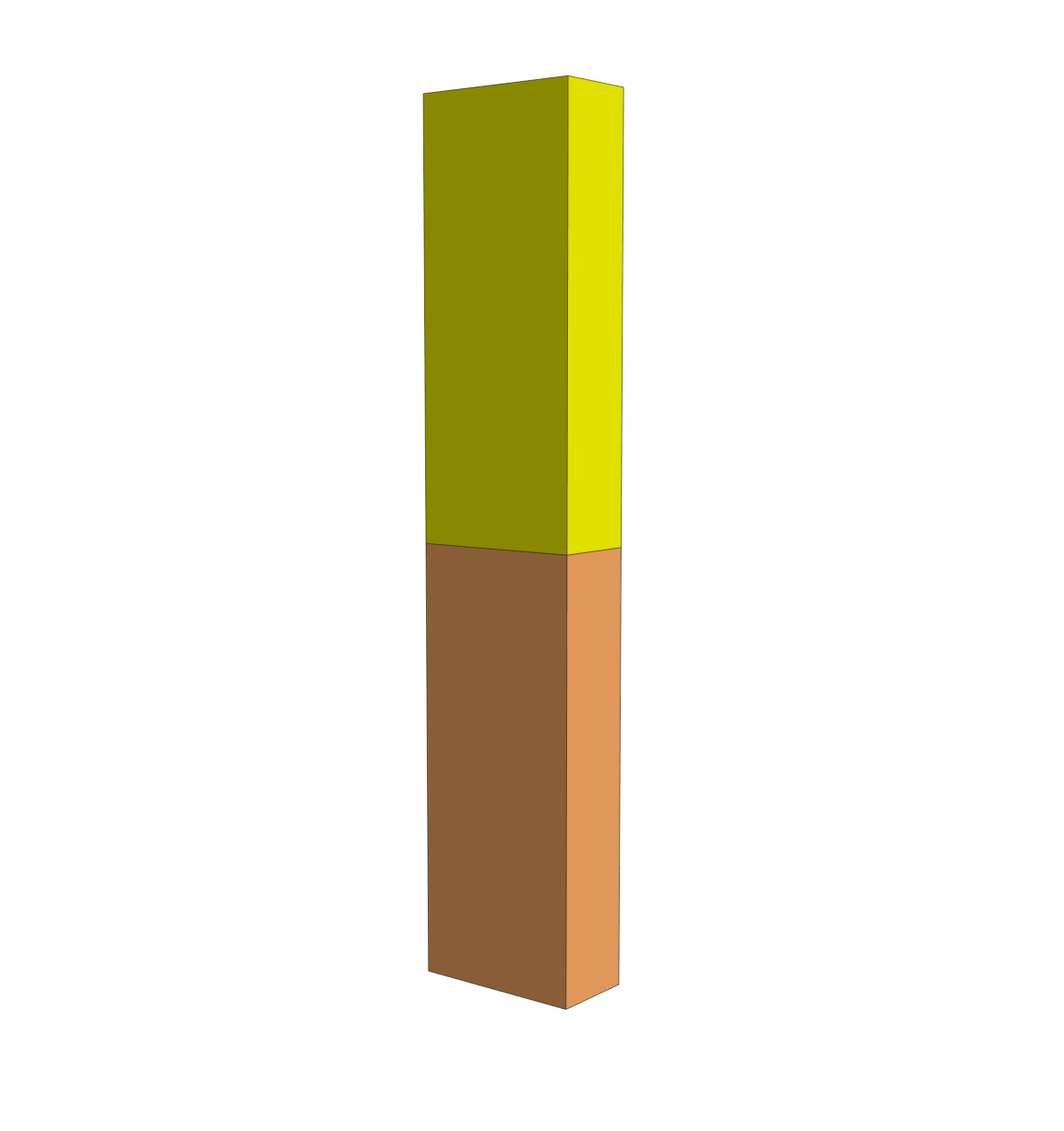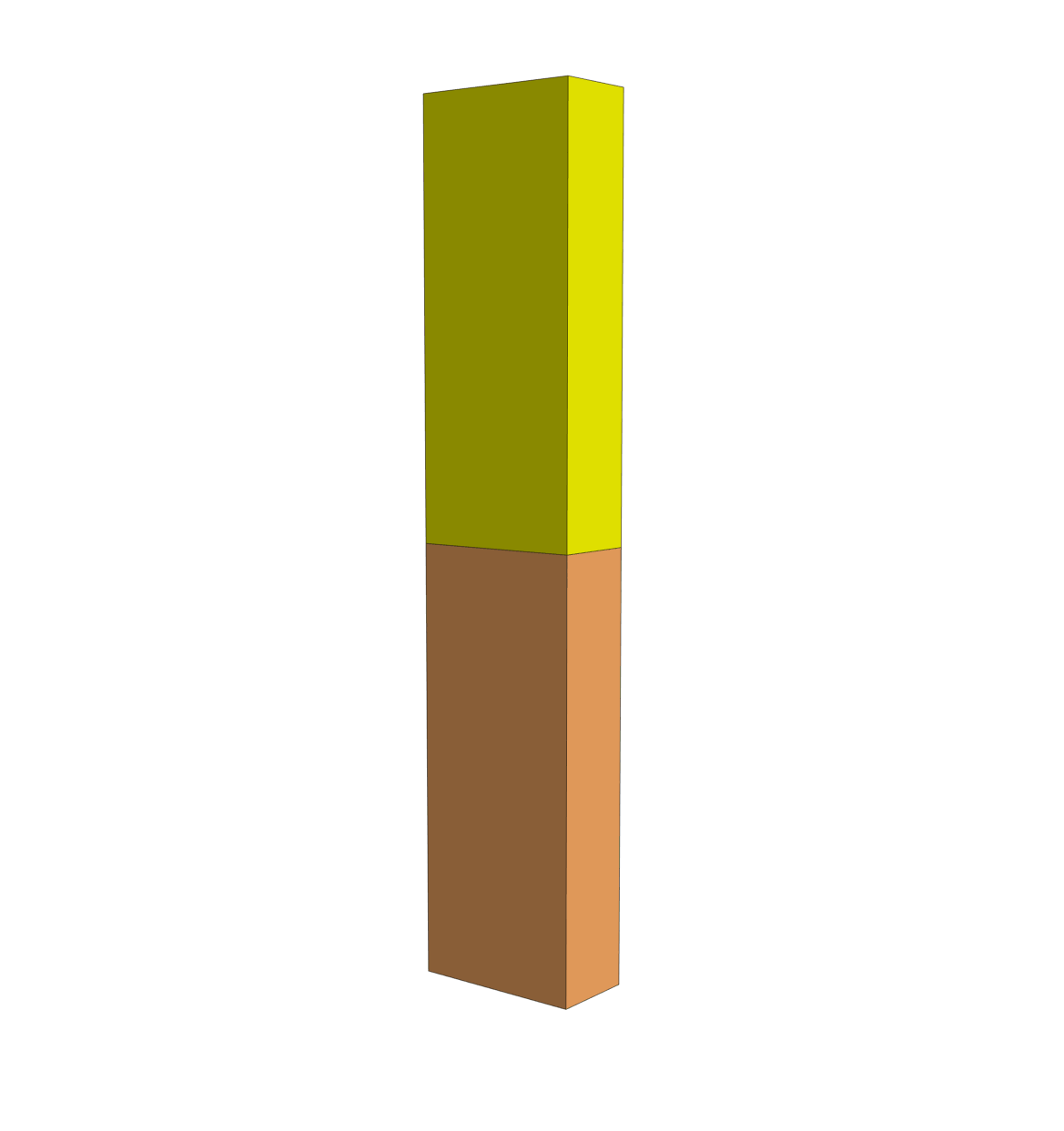
Enforcing \(\pm \frac{\pi}{2}\) radian rotations about the flexion-extension, varus-valgus, and internal-external rotation axes, and \(\pm 1.0\) inferior-superior, medial-lateral, and anterior-posterior translations with rigid connectors. The GhostA and GhostB rigid bodies are hidden.
XPLT Conversion to HDF5
This example demonstrates the conversion of XPLT files to HDF5 format.
In a script:
from pyfebio import xplt
xplt.to_hdf5(inputfile="../../assets/elastic_hex20.xplt", outputfile="elastic_hex20.hdf5")
From the command line in src/examples directory:
python -m pyfebio.xplt ../../assets/elastic_hex20.xplt elastic_hex20.hdf5
One can then interact with the HDF5 file using the h5py package.
For example,
import h5py
def print_datasets(name, obj):
if isinstance(obj, h5py.Dataset):
print(name, f"shape: {obj.shape}", f"dtype: {obj.dtype}")
f = h5py.File("elastic_hex20.hdf5", "r")
# view all the datasets and their shape and dtype
f.visititems(print_datasets)
# shared attributes are stored at the appropriate parent group
# e.g. the time at a given state can be accessed as follows:
print("\n Time at state 5")
print(f["/states/5"].attrs["time"])
# to view the data in a Dataset
print("\n Displacement at state 5")
print(f["/states/5/node_data/displacement/1"][:]) # type: ignore
# this is simply a numpy array so we can also slice it
print("\n Displacement at state 5 of first 2 nodes")
print(f["/states/5/node_data/displacement/1"][0:2, :]) # type: ignore
# the nice thing about this though is HDF5 uses lazy loading
# which means that the data is not loaded into memory until it is accessed
# this is useful for large datasets that do not fit into memory
f.close()
Output:
meshes/0/domains/bottom-layer shape: (1, 21) dtype: int32
meshes/0/domains/top-layer shape: (1, 21) dtype: int32
meshes/0/elementsets/bottom-layer shape: (1,) dtype: int32
meshes/0/elementsets/top-layer shape: (1,) dtype: int32
meshes/0/nodes shape: (32,) dtype: [('id', '<i4'), ('x', '<f4'), ('y', '<f4'), ('z', '<f4')]
meshes/0/nodesets/1 shape: (32,) dtype: int32
meshes/0/nodesets/back shape: (13,) dtype: int32
meshes/0/nodesets/bottom shape: (8,) dtype: int32
meshes/0/nodesets/front shape: (13,) dtype: int32
meshes/0/nodesets/left shape: (13,) dtype: int32
meshes/0/nodesets/right shape: (13,) dtype: int32
meshes/0/nodesets/top shape: (8,) dtype: int32
meshes/0/surfaces/back shape: (2, 10) dtype: int32
meshes/0/surfaces/bottom shape: (1, 10) dtype: int32
meshes/0/surfaces/front shape: (2, 10) dtype: int32
meshes/0/surfaces/left shape: (2, 10) dtype: int32
meshes/0/surfaces/right shape: (2, 10) dtype: int32
meshes/0/surfaces/top shape: (1, 10) dtype: int32
states/0/element_data/stress/bottom-layer shape: (1, 6) dtype: float32
states/0/element_data/stress/top-layer shape: (1, 6) dtype: float32
states/0/mesh/element_state shape: (2,) dtype: int32
states/0/node_data/displacement/1 shape: (32, 3) dtype: float32
states/1/element_data/stress/bottom-layer shape: (1, 6) dtype: float32
states/1/element_data/stress/top-layer shape: (1, 6) dtype: float32
states/1/mesh/element_state shape: (2,) dtype: int32
states/1/node_data/displacement/1 shape: (32, 3) dtype: float32
states/2/element_data/stress/bottom-layer shape: (1, 6) dtype: float32
states/2/element_data/stress/top-layer shape: (1, 6) dtype: float32
states/2/mesh/element_state shape: (2,) dtype: int32
states/2/node_data/displacement/1 shape: (32, 3) dtype: float32
states/3/element_data/stress/bottom-layer shape: (1, 6) dtype: float32
states/3/element_data/stress/top-layer shape: (1, 6) dtype: float32
states/3/mesh/element_state shape: (2,) dtype: int32
states/3/node_data/displacement/1 shape: (32, 3) dtype: float32
states/4/element_data/stress/bottom-layer shape: (1, 6) dtype: float32
states/4/element_data/stress/top-layer shape: (1, 6) dtype: float32
states/4/mesh/element_state shape: (2,) dtype: int32
states/4/node_data/displacement/1 shape: (32, 3) dtype: float32
states/5/element_data/stress/bottom-layer shape: (1, 6) dtype: float32
states/5/element_data/stress/top-layer shape: (1, 6) dtype: float32
states/5/mesh/element_state shape: (2,) dtype: int32
states/5/node_data/displacement/1 shape: (32, 3) dtype: float32
Time at state 5
[1.]
Displacement at state 5
[[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[ 1.1734079e+00 3.4618369e-01 4.2698154e-04]
[ 3.4618369e-01 -1.1734079e+00 4.2698154e-04]
[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[-3.4618369e-01 1.1734079e+00 4.2698154e-04]
[-1.1734079e+00 -3.4618369e-01 4.2698154e-04]
[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[ 1.0007957e+00 9.9920303e-01 0.0000000e+00]
[ 9.9920303e-01 -1.0007957e+00 0.0000000e+00]
[-9.9920303e-01 1.0007957e+00 0.0000000e+00]
[-1.0007957e+00 -9.9920303e-01 0.0000000e+00]
[ 6.8272942e-01 -1.3276277e-01 -1.4378540e-03]
[ 7.6155305e-01 -4.1322845e-01 8.6941756e-03]
[-1.3276277e-01 -6.8272942e-01 -1.4378540e-03]
[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[ 1.3276277e-01 6.8272942e-01 -1.4378540e-03]
[-7.6155305e-01 4.1322845e-01 8.6941756e-03]
[-6.8272942e-01 1.3276277e-01 -1.4378540e-03]
[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[ 4.1322845e-01 7.6155305e-01 8.6941756e-03]
[ 0.0000000e+00 0.0000000e+00 0.0000000e+00]
[-4.1322845e-01 -7.6155305e-01 8.6941756e-03]
[ 1.1713763e+00 6.9261616e-01 2.4284013e-03]
[ 9.9999934e-01 -7.9632644e-04 0.0000000e+00]
[ 6.9261616e-01 -1.1713763e+00 2.4284013e-03]
[-6.9261616e-01 1.1713763e+00 2.4284013e-03]
[-9.9999934e-01 7.9632644e-04 0.0000000e+00]
[-1.1713763e+00 -6.9261616e-01 2.4284013e-03]
[ 7.9632644e-04 9.9999934e-01 0.0000000e+00]
[-7.9632644e-04 -9.9999934e-01 0.0000000e+00]]
Displacement at state 5 of first 2 nodes
[[0.0000000e+00 0.0000000e+00 0.0000000e+00]
[1.1734079e+00 3.4618369e-01 4.2698154e-04]]
OpenKnee Biphasic
Overview
This example uses geometry from the OpenKnee(s) project specimen 003. The femoral and tibial cartilage have been simplified to quadratic triangular (6 node) elements. This substantially reduces computational cost but comes with some concessions. With the current shell capabilities, we can only apply fixed boundary conditions to the bottom shell nodes. This enables us to fix the bottom nodes of the tibial cartilage, since we assume the tibia does not move.
We make the femoral cartilage rigid, so we can move it in the z-direction. Due to this assumption and the lack of menisci, this model overestimates the articular cartilage contact pressure.
Note that we do not include geometry for the femur or tibia, as these are not necessary for this simulation.
Our model simulates creep under compressive loading applied to the femoral rigid body. The default conditions are:
Compressive femoral force of -500 N in the z-direction ramped linearly over 1.0 seconds
-500 N force held constant for 600.0 additional seconds, as the tibial cartilage creeps.
Most simulation parameters are defined as variables at the beginning of the script. Variation of these parameters can be explored, but note that convergence of biphasic analyses can be challenging, so parameters should be changed reasonably.
Some important considerations:
mixed_formulation=1 is defined in the Control section. This utilizes quadratic shape functions for solid displacements and forces, but linear shape functions for the fluid pressures and fluxes. This was found to provide better convergence than using quadratic shape functions for both phases. An argument for this is that Laplace’s equation is of degree 2 while Darcy’s Law is of degree 1.
Broyden’s method is used because our stiffness matrix is non-symmetric
ls_check_jacobians=1 is defined in the Control section. This allows the line search to continue even if a negative Jacobian is encountered. Often a step size can be found to overcome the negative Jacobian(s).
Script
Consult the script code and comments for more details.
from pathlib import Path
import meshio
import pyfebio as feb
# Cartilage thickness (mm)
CARTILAGE_THICKNESS = 1.5
# Solid Phase Material Properties
# EFD NeoHookean
E = 1.0
v = 0.15
fiber_ksi = "10.0,10.0,10.0"
fiber_beta = "2.0,2.0,2.0"
# Fluid Phase Material Properties
# Constant Isotropic Permeability
perm = 1e-3
# Loading
FORCE = -500.0
# Time Parameters
RAMP_TIME = 1.0
HOLD_TIME = 600.0
INITIAL_STEP_SIZE = 0.01
# Must Point spacing increases by this ratio for each point during relaxation phase
INITIAL_MUST_POINT_RELAX_STEP = 1.0
MUST_POINT_RELAX_RATIO = 1.3
assert MUST_POINT_RELAX_RATIO > 1.0, "MUST_POINT_RELAX_RATIO must be greater than 1.0"
assert INITIAL_MUST_POINT_RELAX_STEP > 0.0, "INITIAL_MUST_POINT_RELAX_STEP must be greater than 0.0"
# Relative path to where the mesh files are
base_dir = Path(__file__).parent.joinpath("../../assets/openknee")
# Import the meshes using meshio and assemble into one mesh
element_offset = 0
node_offset = 0
assembled_mesh = feb.mesh.Mesh()
for meshfile in ("fmc.msh", "tbc-l.msh", "tbc-m.msh"):
meshfile = base_dir.joinpath(meshfile)
meshobj = meshio.gmsh.read(meshfile)
febmesh = feb.mesh.translate_meshio(
meshobj,
nodeoffset=node_offset,
elementoffset=element_offset,
shell_sets=["cartilage"],
nodes_name=meshfile.stem,
)
element_offset += febmesh.elements[-1].all_elements[-1].id
node_offset += febmesh.nodes[-1].all_nodes[-1].id
for node in febmesh.nodes:
assembled_mesh.add_node_domain(node)
for i, element in enumerate(febmesh.elements):
if i > 0:
element.name = f"{meshfile.stem}_{i + 2}"
else:
element.name = meshfile.stem
assembled_mesh.add_element_domain(element)
# Part lists for boundary conditions and contact definition later
assembled_mesh.add_part_list(feb.mesh.PartList(name="fmc_list", text="fmc"))
assembled_mesh.add_part_list(feb.mesh.PartList(name="tbc", text="tbc-l,tbc-m"))
## Instatiate a BiphasicModel
# -------------------------------
# mixed_formulation = 1 makes solid phase shape functions quadratic,
# but fluid phase shape functions linear. This demonstrated better behavior
# ls_check_jacobians = 1 does not abort if a negative Jacobian is detected during
# the line search. Often the line search step adjustment can overcome this.
# BroydenMethod() quasi-Newton method for solving the nonlinear system due to
# having a non-symmetric stiffness matrix
model = feb.model.BiphasicModel(
mesh_=assembled_mesh,
control_=feb.control.Control(
analysis="TRANSIENT",
solver=feb.control.BiphasicSolver(mixed_formulation=1, ls_check_jacobians=1, qn_method=feb.control.BroydenMethod()),
step_size=INITIAL_STEP_SIZE,
time_steps=int((HOLD_TIME + RAMP_TIME) / INITIAL_STEP_SIZE + 0.5),
time_stepper=feb.control.TimeStepper(dtmax=feb.control.TimeStepValue(lc=1)),
plot_level="PLOT_MUST_POINTS",
),
)
# ----------------------------------
## Material Definition
# ----------------------------------
# Loop over Elements() and assign materials
for i, element in enumerate(model.mesh_.elements[1:3]):
solid = feb.material.EllipsoidalFiberDistributionNeoHookean(
E=feb.material.MaterialParameter(text=E),
v=feb.material.MaterialParameter(text=v),
ksi=feb.material.MaterialParameter(text=fiber_ksi),
beta=feb.material.MaterialParameter(text=fiber_beta),
)
mat = feb.material.BiphasicMaterial(
name=element.name,
id=i + 1,
permeability=feb.material.ConstantIsoPerm(
perm=feb.material.MaterialParameter(text=perm),
),
solid=solid,
)
model.material_.add_material(mat)
model.meshdomains_.add_shell_domain(
feb.meshdomains.ShellDomain(name=element.name, mat=element.name, shell_thickness=CARTILAGE_THICKNESS)
)
# Assign a rigid body material to the femoral cartilage
# Note material properties and thicknesses are used when
# calculating the auto_penalty for contact
mat = feb.material.RigidBody(
name="fmc",
id=3,
center_of_mass="0.0,0.0,0.0",
E=feb.material.MaterialParameter(text=E * 5.0),
v=feb.material.MaterialParameter(text=v),
)
model.material_.add_material(mat)
model.meshdomains_.add_shell_domain(feb.meshdomains.ShellDomain(name="fmc", mat="fmc", shell_thickness=CARTILAGE_THICKNESS))
# ----------------------------------
# Fix bottom nodes of tibial cartilage shells in space
model.boundary_.add_bc(feb.boundary.BCZeroShellDisplacement(node_set="@part_list:tbc", sx_dof=1, sy_dof=1, sz_dof=1))
# Fix the fmc rigid body in all DoFs but z
model.rigid_.add_rigid_bc(feb.rigid.RigidFixed(rb="fmc", Rx_dof=1, Ry_dof=1, Rz_dof=0, Ru_dof=1, Rw_dof=1, Rv_dof=1))
# Apply a compressive force to the fmc rigid body in the z direction
model.rigid_.add_rigid_load(feb.rigid.RigidForceLoad(rb="fmc", dof="Rz", value=feb.rigid.Value(lc=2, text=FORCE), load_type=1))
## Add Biphasic Sliding Contact Constraint
# -----------------------------------------
# Surface Pair for Biphasic Sliding Contact Constraint
model.mesh_.add_surface_pair(feb.mesh.SurfacePair(name="fmc_tbc", primary="@part_list:tbc", secondary="@part_list:fmc_list"))
# Biphasic Sliding Contact Constraint
# gaptol is fairly strict at 0.1mm
# this yielded better behavior than softer contact enforcement
model.contact_.add_contact(
feb.contact.SlidingBiphasic(
surface_pair="fmc_tbc",
auto_penalty=1,
laugon="AUGLAG",
gaptol=0.1,
tolerance=0,
symmetric_stiffness=0,
search_radius=2.0,
two_pass=1,
)
)
# -----------------------------------------
# Load Curves
# -----------------------------------------
# Must Point Load Curve Definition
must_points = [f"{RAMP_TIME},{RAMP_TIME}"]
elapsed_time = RAMP_TIME
step = INITIAL_MUST_POINT_RELAX_STEP
elapsed_time += step
terminate = 1
while terminate >= 0:
must_points.append(f"{elapsed_time},{step}")
step *= MUST_POINT_RELAX_RATIO
elapsed_time += step
if elapsed_time > RAMP_TIME + HOLD_TIME:
elapsed_time = RAMP_TIME + HOLD_TIME
terminate -= 1
model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=1, interpolate="STEP", extend="CONSTANT", points=feb.loaddata.CurvePoints(points=must_points))
)
# Force Load Curve Definition
model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(
id=2,
interpolate="LINEAR",
extend="CONSTANT",
points=feb.loaddata.CurvePoints(points=["0.0,0.0", f"{RAMP_TIME},1.0", f"{RAMP_TIME + HOLD_TIME},1.0"]),
)
)
# -----------------------------------------
# Requested Plot Variables
model.output_.add_plotfile(
feb.output.OutputPlotfile(
all_vars=[
feb.output.Var(type="shell strain"),
feb.output.Var(type="stress"),
feb.output.Var(type="shell relative volume"),
feb.output.Var(type="contact pressure"),
feb.output.Var(type="contact gap"),
feb.output.Var(type="effective fluid pressure"),
feb.output.Var(type="fluid flux"),
feb.output.Var(type="displacement"),
]
)
)
# Save and run the model
model.save("openknee_biphasic.feb")
_ = feb.model.run_model(filepath="openknee_biphasic.feb")
Example Results
Simulations of -500 N compression applied over 1.0 seconds and held for 600 additional seconds. Notice the relative volume change of the tibial cartilage shell elements as the cartilage creeps. The vectors represent the current fluid fluxes dynamically scaled to the value range in each time step. Likewise, the relative volume colors are dynamically adjusted. Click the image for full-size.
OpenKnee Elastic
TL;DR
Run the example with default settings:
python openknee_elastic.py
See help for CLI arguments:
python openknee_elastic.py --help
Overview
This example uses geometry from the OpenKnee(s) project specimen 003. The femoral and tibial cartilage have been simplified to quadratic triangular (6 node) elements. This substantially reduces computational cost but comes with some concessions. With the current shell capabilities, we can only apply fixed boundary conditions to the bottom shell nodes. This enables us to fix the bottom nodes of the tibial cartilage, since we assume the tibia does not move. The femoral geometry is included just for visualization, and has no effect on then simulation.
We defined a pydantic BaseModel to configure the model parameters. Possibly of interest , we have defined a flag to choose between 3 levels of mesh refinement:
COARSE (3mm edge),
MEDIUM (2mm edge), and
FINE (1mm edge),
which have substantially differing computational cost.
FEBio Features Demonstrated:
Multistep Analysis
Shell Boundary Conditions
Rigid Cylindrical Joints
Discrete nonlinear spring definition
A Blankevoort spring model defined using the string expression with appropriate Heaviside functions to make tension-only with a toe region and allow for prestrain definition
Additional Techniques Demonstrated:
Defining a pydantic BaseModel for this particular study configuration
Creating a parser that allows for overriding some configuration parameters from the command line interface
Simulation Details:
Global Settings and Components:
Contact between the femoral and tibial cartilage is defined as SlidingElastic and enforced with the augmented Lagrangian method
The tibia is fixed in space
The bottom nodes of the tibial cartilage shells are fixed in space.
The femoral cartilage is rigidly constrained to the femoral rigid body.
The ligaments are defined based on a LigamentConfig model. The default configuration is contained in ligament.json
Step 1: A compressive load is applied to the femur in the Z-direction with rotation about the X-axis fixed and all other DoF free.
Step 2: The compressive load from Step 1 is kept constant, but a chain of 3 cylindrical joints is defined to control relative rigid body motion in the convention of Grood and Suntay (1983).
The chain starts at the tibia rigid body, which is fixed in space.
The tibiaGhost rigid body is constrained to translate along and rotate about the IE_rot_IS_translation (E3) cylindrical axis relative to the tibia rigid body.
The femurGhost rigid body is constrained to translate along and rotate about the VV_rot_AS_translation (E2) cylindrical axis relative to the tibiaGhost rigid body.
The femur rigid body is constrained to translate along and rotate about the Flexion_rot_ML_translation (E1) cylindrical axis relative to the femurGhost rigid body.
The flexion angle is prescribed, while all other joint DoFs are left free.
Script
Consult the script code and comments for more details:
import argparse
import json
from pathlib import Path
from typing import Literal
import meshio
from pydantic import BaseModel, Field
import pyfebio as feb
class LigamentModel(BaseModel, frozen=True):
proximal: list[tuple[float, float, float]]
distal: list[tuple[float, float, float]]
youngs_modulus: float = Field(gt=0.0)
area: float = Field(gt=0.0)
lambda0: float = Field(gt=0.0)
prestretch: float = Field(gt=0.0)
class LigamentConfig(BaseModel, frozen=True):
ligaments: dict[str, LigamentModel]
class ModelConfig(BaseModel, frozen=True):
# Directory containing mesh files
mesh_directory: str | Path = "../../assets/openknee"
# Mesh resolution flag. Max edge lengths as follows:
# COARSE: 3.0mm
# MEDIUM: 2.0mm
# FINE: 1.0mm
mesh_resolution: Literal["COARSE", "MEDIUM", "FINE"] = "MEDIUM"
# Femur and Tibia origins. Defaults from OpenKnee model 003
femur_origin: tuple[float, float, float] = (-1.036, -6.717, 0.171)
tibia_origin: tuple[float, float, float] = (-4.4315, -7.2204999999999995, -24.9345)
# Grood and Suntay axes e1, e2, e3. From OpenKnee model 003, but e1,e2 corrected
# for a left knee
e1: tuple[float, float, float] = (-0.9889108468842679, 0.1485103932882822, 0.0)
e2: tuple[float, float, float] = (-0.1485103932882822, -0.9889108468842679, 0.0)
e3: tuple[float, float, float] = (0.0, 0.0, 1.0)
# Cartilage thickness in mm
cartilage_thickness: float = Field(default=1.5, gt=0.0)
# Young's modulus of the cartilage material in MPa
youngs_modulus: float = Field(default=10.0, gt=0.0)
# Poisson's ratio of the cartilage material
# if poissons_ratio >= 4.5 an uncoupled Mooney-Rivlin model is used
# otherwise a compressible Neo-Hookean model is used
poissons_ratio: float = Field(default=0.4, ge=0.0)
# Ligament configuration file
ligament_config: str = "ligaments.json"
superior_load: float = -500.0
flexion_angle: float = 1.57 / 2.0
# Contact gap tolerance in mm enforced by the Augmented Lagrangian method
contact_gap: float = 0.1
# Angle tolerance in radians for connector constraints
connector_angle_tolerance: float = 0.0005
# Gap tolerance in mm for connector constraints
connector_gap_tolerance: float = 0.05
output_vars: list[feb.output.PlotDataVariables] = [
"displacement",
"stress",
"Lagrange strain",
"shell strain",
"contact pressure",
"contact gap",
"shell relative volume",
"discrete element force",
"discrete element stretch",
]
model_config = ModelConfig()
with open(model_config.ligament_config) as f:
ligament_config = ModelConfig(**json.load(f))
def import_and_assemble_mesh(mesh_directory: str | Path, mesh_resolution: Literal["COARSE", "MEDIUM", "FINE"]) -> feb.mesh.Mesh:
"""
Imports the appropriate mesh files based on provided mesh_resolution and mesh_directory.
Assembles the meshes into a single pyfebio Mesh object.
"""
suffix = {"COARSE": "_3p0.msh", "MEDIUM": "_2p0.msh", "FINE": ".msh"}
element_offset = 0
node_offset = 0
assembled_mesh = feb.mesh.Mesh()
for name in ("tbc-l", "tbc-m", "fmc", "femur"):
if name != "femur":
meshfile = Path(mesh_directory).joinpath(f"{name}{suffix[mesh_resolution]}")
else:
meshfile = Path(mesh_directory).joinpath(f"{name}.msh")
meshobj = meshio.gmsh.read(meshfile)
febmesh = feb.mesh.translate_meshio(
meshobj, nodeoffset=node_offset, elementoffset=element_offset, shell_sets=["cartilage"], nodes_name=name
)
element_offset = febmesh.elements[-1].all_elements[-1].id
node_offset = febmesh.nodes[-1].all_nodes[-1].id
for node in febmesh.nodes:
assembled_mesh.add_node_domain(node)
for i, element in enumerate(febmesh.elements):
if i > 0:
element.name = f"{name}_{i + 2}"
else:
element.name = name
assembled_mesh.add_element_domain(element)
assembled_mesh.add_part_list(feb.mesh.PartList(name="fmc_list", text="fmc"))
assembled_mesh.add_part_list(feb.mesh.PartList(name="femur_list", text="femur"))
assembled_mesh.add_part_list(feb.mesh.PartList(name="tbc", text="tbc-l,tbc-m"))
return assembled_mesh
def define_ligaments(model: feb.model.Model, ligament_model: LigamentConfig) -> None:
"""
Defines the ligaments for the model based on the provided LigamentConfig pydantic BaseModel.
"""
node_offset = model.mesh_.nodes[-1].all_nodes[-1].id + 1
element_offset = model.mesh_.elements[-1].all_elements[-1].id + 1
# Iterate over the ligaments dict keys and values
# Each key serves as the element, domain, and material name
# The values are LigamentModel instances. Consult the LigamentModel class definition for details.
for discrete_id, (name, ligament) in enumerate(ligament_model.ligaments.items()):
# Instantiate Nodes objects for the proximal and distal nodes
proximal_nodes = feb.mesh.Nodes(name=f"{name}_proximal")
distal_nodes = feb.mesh.Nodes(name=f"{name}_distal")
# Instantiate DiscreteSet object for the spring elements representing the ligament
discrete_set = feb.mesh.DiscreteSet(name=name)
n_fibers = len(ligament.proximal)
for prox_node, dist_node in zip(ligament.proximal, ligament.distal):
proximal_nodes.add_node(feb.mesh.Node(id=node_offset, text=f"{prox_node[0]},{prox_node[1]},{prox_node[2]}"))
distal_nodes.add_node(feb.mesh.Node(id=node_offset + n_fibers, text=f"{dist_node[0]},{dist_node[1]},{dist_node[2]}"))
discrete_set.add_element(new_element=feb.mesh.DiscreteElement(text=f"{node_offset},{node_offset + n_fibers}"))
# offset the element and node counters
element_offset += 1
node_offset += 1
# need to offset nodes by 2 after the loop is completed
node_offset += 2
# Add the node and discrete sets to the model mesh_
model.mesh_.add_node_domain(proximal_nodes)
model.mesh_.add_node_domain(distal_nodes)
model.mesh_.add_discrete_set(discrete_set)
# Define a Blankevoort spring model using configuration parameters and
# the NonLinearSpring discrete material referencing a math expression
prestrain = ligament.prestretch - 1.0
e0 = ligament.lambda0 - 1.0
toe_region = f"H(x + {prestrain:.5f}) * ({0.5 / e0:.5f} * (x + {prestrain:.5f}) ^ 2) * (1.0 - H(x + {prestrain - e0:.5f}))"
linear_region = f"H(x + {prestrain - e0:.5f}) * (x + {prestrain - e0 / 2.0:.5f})"
dmat = feb.discrete.NonlinearSpring(
id=discrete_id + 1,
name=name,
scale=ligament.youngs_modulus * ligament.area,
measure="strain",
force=feb.discrete.NonlinearSpringForce(math=f"{toe_region} + {linear_region}"),
)
# Add the material and element to the model discrete_ section
model.discrete_.add_discrete_material(dmat)
model.discrete_.add_discrete_element(feb.discrete.DiscreteEntry(dmat=discrete_id + 1, discrete_set=name))
def main(model_config: ModelConfig, quiet: bool = False) -> None:
# Construct the ligament configuration object from JSON file
with open(model_config.ligament_config, "r") as f:
ligament_config = LigamentConfig(**json.load(f))
assembled_mesh = import_and_assemble_mesh(model_config.mesh_directory, model_config.mesh_resolution)
model = feb.model.Model(
mesh_=assembled_mesh,
control_=None,
)
# Shear modulus and bulk modulus from E and v
G: float = model_config.youngs_modulus / (2 * (1 + model_config.poissons_ratio))
K: float = model_config.youngs_modulus / (3 - 6 * model_config.poissons_ratio)
for i, element in enumerate(model.mesh_.elements[0:3]):
# Use an Uncoupled Mooney-Rivlin material if nearly incompressible
# otherwise use a Neo-Hookean material
if model_config.poissons_ratio >= 0.45:
mat = feb.material.MooneyRivlinUC(
name=element.name,
id=i + 1,
c1=feb.material.MaterialParameter(text=G / 2.0),
c2=feb.material.MaterialParameter(text=0.0),
k=feb.material.MaterialParameter(text=K),
)
else:
mat = feb.material.NeoHookean(
name=element.name,
id=i + 1,
E=feb.material.MaterialParameter(text=model_config.youngs_modulus),
v=feb.material.MaterialParameter(text=model_config.poissons_ratio),
)
model.material_.add_material(mat)
model.meshdomains_.add_shell_domain(
feb.meshdomains.ShellDomain(name=element.name, mat=element.name, shell_thickness=model_config.cartilage_thickness)
)
# Make the femur Elements a rigid body
mat = feb.material.RigidBody(
name="femur",
id=4,
center_of_mass=f"{model_config.femur_origin[0]},{model_config.femur_origin[1]},{model_config.femur_origin[2]}",
E=feb.material.MaterialParameter(text=model_config.youngs_modulus),
v=feb.material.MaterialParameter(text=model_config.poissons_ratio),
)
model.material_.add_material(mat)
model.meshdomains_.add_shell_domain(
feb.meshdomains.ShellDomain(name="femur", mat="femur", shell_thickness=model_config.cartilage_thickness)
)
# Ligaments
# --------------------------------------------------------------
define_ligaments(model, ligament_config)
for ligament in ligament_config.ligaments:
model.boundary_.add_bc(feb.boundary.BCRigid(node_set=f"{ligament}_proximal", rb="femur"))
model.boundary_.add_bc(feb.boundary.BCZeroDisplacement(node_set=f"{ligament}_distal", x_dof=1, y_dof=1, z_dof=1))
# --------------------------------------------------------------
# Create simple rigid bodies for the tibia, tibiaGhose, and femurGhost parts
# --------------------------------------------------------------
floating_origin = [(a + b) / 2.0 for a, b in zip(model_config.femur_origin, model_config.tibia_origin)]
model.add_simple_rigid_body(origin=(floating_origin[0], floating_origin[1], floating_origin[2]), name="femurGhost")
model.add_simple_rigid_body(origin=(floating_origin[0], floating_origin[1], floating_origin[2]), name="tibiaGhost")
model.add_simple_rigid_body(
origin=(model_config.tibia_origin[0], model_config.tibia_origin[1], model_config.tibia_origin[2]), name="tibia"
)
# --------------------------------------------------------------
# Global (all steps) Boundary conditions and Contact interactions
# --------------------------------------------------------------
model.boundary_.add_bc(feb.boundary.BCRigid(node_set="@part_list:fmc_list", rb="femur"))
model.boundary_.add_bc(feb.boundary.BCZeroShellDisplacement(node_set="@part_list:tbc", sx_dof=1, sy_dof=1, sz_dof=1))
model.rigid_.add_rigid_bc(feb.rigid.RigidFixed(rb="tibia", Rx_dof=1, Ry_dof=1, Rz_dof=1, Ru_dof=1, Rw_dof=1, Rv_dof=1))
model.mesh_.add_surface_pair(feb.mesh.SurfacePair(name="fmc_tbc", primary="@part_list:tbc", secondary="@part_list:fmc_list"))
model.contact_.add_contact(
feb.contact.SlidingElastic(
surface_pair="fmc_tbc",
penalty=10.0,
laugon="AUGLAG",
gaptol=model_config.contact_gap,
two_pass=1,
search_radius=2.0,
tolerance=0,
symmetric_stiffness=0,
)
)
# --------------------------------------------------------------
# Define the first step (prestrain)
# --------------------------------------------------------------
model.step_.add_step(
feb.step.StepEntry(
id=1,
control=feb.control.Control(
solver=feb.control.SolidSolver(qn_method=feb.control.BroydenMethod(), lsiter=10),
time_steps=10,
step_size=0.1,
time_stepper=feb.control.TimeStepper(dtmax=feb.control.TimeStepValue(lc=1), max_retries=5),
plot_level="PLOT_MUST_POINTS",
),
name="prestrain",
rigid=feb.rigid.Rigid(),
)
)
# Fix the femur in rotation about x-axis
model.step_.all_steps[0].rigid.add_rigid_bc(
feb.rigid.RigidFixed(rb="femur", Rx_dof=0, Ry_dof=0, Rz_dof=0, Ru_dof=1, Rw_dof=0, Rv_dof=0)
)
# Apply a compressive load in the z-direction
model.step_.all_steps[0].rigid.add_rigid_load(
feb.rigid.RigidForceLoad(rb="femur", dof="Rz", value=feb.rigid.Value(lc=2, text=model_config.superior_load))
)
# --------------------------------------------------------------
# Define the second step (load)
# --------------------------------------------------------------
model.step_.add_step(
feb.step.StepEntry(
id=2,
name="load",
control=feb.control.Control(
solver=feb.control.SolidSolver(qn_method=feb.control.BroydenMethod(), lsiter=10),
time_steps=100,
step_size=0.01,
time_stepper=feb.control.TimeStepper(dtmax=feb.control.TimeStepValue(lc=1), max_retries=5),
plot_level="PLOT_MUST_POINTS",
),
rigid=feb.rigid.Rigid(),
)
)
# Define the internal-external rotation, inferior-superior translation cylindrical joint
# This is Grood-Suntay E3
model.step_.all_steps[1].rigid.add_rigid_connector(
feb.rigid.RigidCylindricalJoint(
name="IE_rot_IS_translation",
body_a="tibia",
body_b="tibiaGhost",
joint_origin=f"{model_config.tibia_origin[0]},{model_config.tibia_origin[1]},{model_config.tibia_origin[2]}",
joint_axis=f"{model_config.e3[0]},{model_config.e3[1]},{model_config.e3[2]}",
auto_penalty=1,
laugon="AUGLAG",
gaptol=model_config.connector_gap_tolerance,
angtol=model_config.connector_angle_tolerance,
tolerance=0,
)
)
# Define the varus-valgus rotation, anterior-posterior translation cylindrical joint
# This is Grood-Suntay E2
model.step_.all_steps[1].rigid.add_rigid_connector(
feb.rigid.RigidCylindricalJoint(
name="VV_rot_AP_translation",
body_a="tibiaGhost",
body_b="femurGhost",
joint_origin=f"{floating_origin[0]},{floating_origin[1]},{floating_origin[2]}",
joint_axis=f"{model_config.e2[0]},{model_config.e2[1]},{model_config.e2[2]}",
auto_penalty=1,
gaptol=model_config.connector_gap_tolerance,
angtol=model_config.connector_angle_tolerance,
laugon="AUGLAG",
tolerance=0,
)
)
# Define the flexion-extension, medial-lateral translation cylindrical joint
# This is Grood-Suntay E1
model.step_.all_steps[1].rigid.add_rigid_connector(
feb.rigid.RigidCylindricalJoint(
name="Flexion_rot_ML_translation",
body_a="femurGhost",
body_b="femur",
joint_origin=f"{model_config.femur_origin[0]},{model_config.femur_origin[1]},{model_config.femur_origin[2]}",
joint_axis=f"{model_config.e1[0]},{model_config.e1[1]},{model_config.e1[2]}",
auto_penalty=1,
laugon="AUGLAG",
gaptol=model_config.connector_gap_tolerance,
angtol=model_config.connector_angle_tolerance,
tolerance=0,
prescribed_rotation=1,
rotation=feb.rigid.Value(lc=3, text=model_config.flexion_angle),
)
)
# Apply the same compressive load to the femur as in prestrain step
model.step_.all_steps[1].rigid.add_rigid_load(
feb.rigid.RigidForceLoad(rb="femur", dof="Rz", value=feb.rigid.Value(lc=2, text=-model_config.superior_load))
)
# --------------------------------------------------------------
# Define the Load Curves
# --------------------------------------------------------------
# must points forcing output at the 1.0 (end of prestrain step)
# and at every 0.1 seconds during the load step
must_points = ["1.0,1.0"]
must_points += [f"{1.0 + (i + 1) * 0.1},0.1" for i in range(10)]
model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(
id=1,
interpolate="STEP",
points=feb.loaddata.CurvePoints(points=must_points),
)
)
# Load curve scaling the compressive femoral force
model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(
id=2,
interpolate="LINEAR",
points=feb.loaddata.CurvePoints(points=["0.0,0.0", "1.0,1.0"]),
)
)
# Load curve defining the femoral rotation via rigid connnector Flexion_rot_ML_translation
model.loaddata_.add_load_curve(
feb.loaddata.LoadCurve(id=3, interpolate="LINEAR", points=feb.loaddata.CurvePoints(points=["1.0,0.0", "2.0,1.0"]))
)
# --------------------------------------------------------------
# Request plot variables listed in ModelConfig
model.output_.add_plotfile(feb.output.OutputPlotfile(all_vars=[feb.output.Var(type=v) for v in model_config.output_vars]))
# Save and Run the Model
output_name = f"openknee_elastic_{model_config.mesh_resolution.lower()}.feb"
model.save(output_name)
success = feb.model.run_model(filepath=output_name, silent=quiet)
if success == 0:
print(f"Model: {output_name} run successful.")
else:
print(f"Model: {output_name} run failed.")
if __name__ == "__main__":
# Configure a parser to allow for CLI execution and control
parser = argparse.ArgumentParser()
parser.add_argument("--config", type=str, help="path to configuration file")
parser.add_argument("--quiet", action="store_true", help="Disable most most screen messages.")
parser.add_argument("--mesh_resolution", choices=["COARSE", "MEDIUM", "FINE"], help="Override mesh resolution")
parser.add_argument("--ligament_config", type=str, help="Override path to ligament configuration file")
parser.add_argument("--youngs_modulus", type=float, help="Override Young's modulus")
parser.add_argument("--poissons_ratio", type=float, help="Override Poisson's ratio")
parser.add_argument("--superior_load", type=float, help="Override force to apply in z-direction")
parser.add_argument("--flexion_angle", type=float, help="Override flexion angle to apply in second step (in radians)")
args = parser.parse_args()
# If no config file is provided, use the default ModelConfig
# Otherwise, load the config from the provided file using json package
if args.config is None:
model_config = ModelConfig()
else:
with open(args.config, "r") as f:
model_config = ModelConfig(**json.load(f))
# Update the model_config with any CLI arguments
update_dict = {}
for arg, value in vars(args).items():
if value is not None and arg not in ["config", "quiet"]:
update_dict[arg] = value
model_config = model_config.model_copy(update=update_dict)
# Run the main function
main(model_config=model_config, quiet=args.quiet)
Ligament Configuration
The default ligament configuration is shown below:
{
"ligaments": {
"LCL": {
"proximal": [
[36.2065, 3.61435, -8.37739],
[34.914, 7.70706, -7.86844]
],
"distal": [
[48.9634, 11.7753, -55.9914],
[49.0091, 16.5223, -55.4169]
],
"prestretch": 1.03,
"area": 15.0,
"youngs_modulus": 400.0,
"lambda0": 1.05
},
"Popliteus": {
"proximal": [
[34.676, 14.1625, -14.9737],
[33.731, 15.7294, -8.30712]
],
"distal": [
[-13.085, 10.4192, -64.4261],
[-19.1438, 15.9998, -54.9774]
],
"prestretch": 1.03,
"area": 10.0,
"youngs_modulus": 400.0,
"lambda0": 1.05
},
"MCL": {
"proximal": [
[-34.2106, 15.6584, -8.48661],
[-38.6504, 3.52059, -3.15893]
],
"distal": [
[-20.862, 12.0494, -55.7362],
[-21.7085, 4.14904, -56.8732]
],
"prestretch": 1.02,
"area": 20.0,
"youngs_modulus": 400.0,
"lambda0": 1.05
},
"ACL_AMB": {
"proximal": [
[4.56917, 7.17954, 0.708925],
[8.52209, 9.78212, 0.298689]
],
"distal": [
[4.56273, -8.46126, -30.8567],
[8.5027, -5.36515, -31.9216]
],
"prestretch": 1.03,
"area": 15.0,
"youngs_modulus": 400.0,
"lambda0": 1.05
},
"ACL_PLB": {
"proximal": [
[12.7584, 15.2946, -0.904934],
[10.5101, 11.7358, -0.112561]
],
"distal": [
[4.16425, -7.96197, -30.7149],
[-0.349396, -9.32113, -29.0721]
],
"prestretch": 1.03,
"area": 15.0,
"youngs_modulus": 400.0,
"lambda0": 1.05
},
"PCL_PMB": {
"proximal": [
[-4.13125, -1.18167, -18.4196],
[-6.12502, 3.29876, -15.0354]
],
"distal": [
[5.18932, 20.0733, -36.0148],
[1.07589, 21.6042, -36.8836]
],
"prestretch": 0.7,
"area": 5.0,
"youngs_modulus": 400.0,
"lambda0": 1.05
},
"PCL_ALB": {
"proximal": [
[1.27595, -3.55716, -16.7215],
[-4.01803, -1.19421, -17.8023]
],
"distal": [
[4.7901, 18.7831, -34.7463],
[0.654849, 18.4743, -35.7122]
],
"prestretch": 0.7,
"area": 5.0,
"youngs_modulus": 400.0,
"lambda0": 1.05
}
}
}
Example Results
Simulations using the FINE and COARSE meshes with default settings: -500 N compression, 45° flexion. Click the image for full-size.